2020.04.16
考试干货 · 来自于PC
9058


本章介绍了财务管理最基础的几个概念,准确理解掌握有利于大家对后续章节的学习。
货币时间价值,体现了一种折现的思想,债券、股票的价值其实就是未来现金流量的现值,项目的投资决策中现金流量的确定也需用到折现。学习时,建议大家结合时间轴去分析各期的资金流动情况。
在投资过程中,风险与收益如影随形,我们要对其进行识别、衡量,尤其要掌握的是资本资产定价模型。
成本性态,是对成本与业务量之间的依存关系进行分析,从而在数量上具体掌握成本与业务量之间的规律性关系,以便为企业正确地进行最优管理决策和改善经营管理提供有价值的资料。

第一节 货币时间价值
(一)货币时间价值的概念
货币时间价值,是指在没有风险和没有通货膨胀的情况下,货币经历一定时间的投资和再投资所增加的价值,也称为资金的时间价值。

(二)终值和现值
1. 终值(又称将来值):是指当前的一定量资金在若干期后所具有的价值,通常记作 F。
2. 现值:是指未来某一时点一定量的资金折算到当前(基准时点)所具有的价值,通常记作 P。
3. 现值和终值是一定量货币在前后两个不同时点上对应的价值,其差额即为货币时间价值。


(一)单利和复利
单利和复利是计算利息的两种方式。
1. 单利:指按照固定的本金计算利息的一种计息方式,所生利息均不加入本金重复计算利息

2. 复利:指不仅对本金计算利息,还将各期的利息加入本金再去计算下期利息的一种逐期滚动计算方式。

(二)复利终值和现值
1. 复利终值:指一定量的货币,按复利计算的若干期后的本利总和。复利终值的计算公式为:
F = P (1 + i ) n = P ×( F/P,i,n )
式中, n 为计息期数; i 为计息期利率;(1 + i ) n 为复利终值系数,记作( F/P,i,n ),考试时通常会直接给出;本书附录中也会给出大家常用的复利终值系数表。
2. 复利现值:指未来某期的一定量的货币,按复利计算方式折算到现在的价值。复利现值的计算公式为:
P =F(1 + i ) n= F ×( P/F,i,n )
式中, n 为计息期数;1(1 + i ) n为复利现值系数,记作( P/F,i,n ) ,考试时通常会直接给出;


(一)年金的概述
1. 年金(annuity):指间隔期相等的系列等额收付款项,一般用 A 表示。利息、租金、保险费等通常表现为年金的形式。
2. 年金的类别
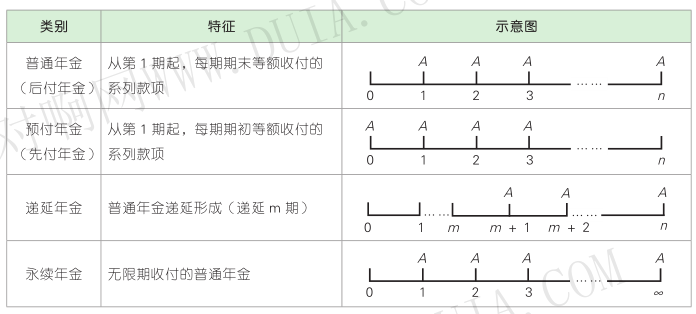

(二)年金终值( F)
1.普通年金终值(后付年金终值)
(1)普通年金终值:对于等额收付 n 次的普通年金而言,其终值指的是各期等额收付金额在第 n 期期末的复利终值之和。
(2)普通年金终值的计算公式为:

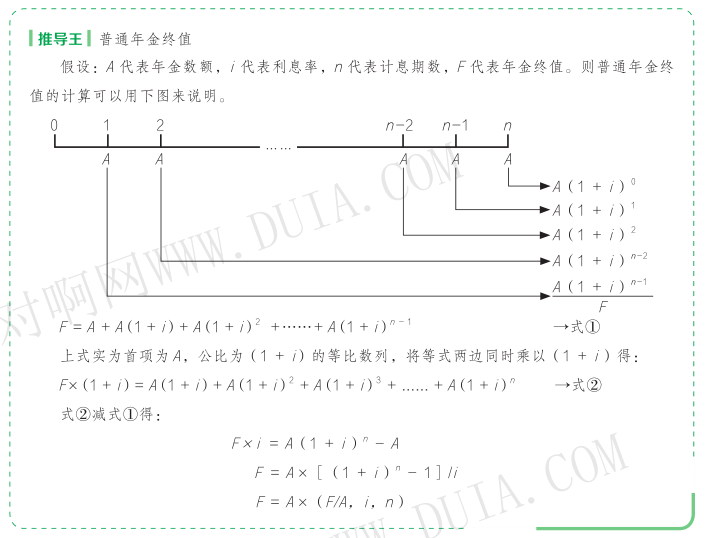

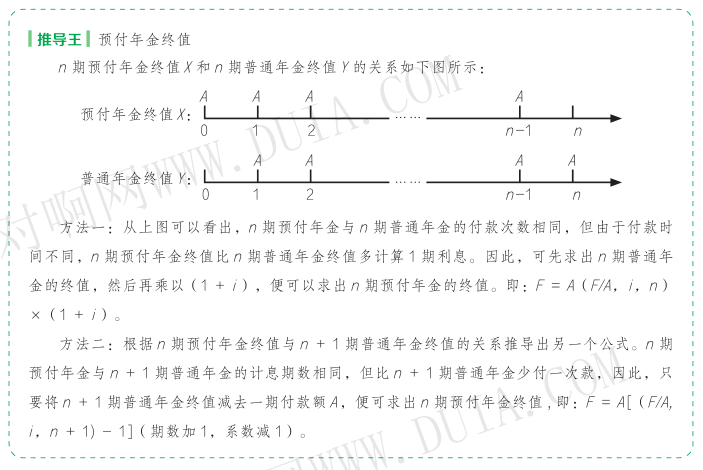
2. 预付年金终值(先付年金终值或即付年金终值)
(1)预付年金终值:对于等额收付 n 次的预付年金而言,其终值指的是各期等额收付金额在第 n 期期末的复利终值之和。由于最常见的是普通年金,所以年金终值系数表和年金现值系数表,一般只提供普通年金的。因此,为了便于计算和查表,我们就必须找到普通年金和预付年金之间系数的转化关系。
(2)预付年金终值的计算公式:
F = A ( F/A,i,n )×(1 + i )
或 F = A [( F/A,i,n + 1)- 1](期数加 1,系数减 1)

3. 递延年金终值
(1)对于递延期为 m 、等额收付 n 次的递延年金而言,其终值指的是各期等额收付金额在第( m + n )期期末的复利终值之和。
(2)计算公式为:
F = A ( F / A , i,n )

4. 永续年金没有终值
永续年金的期限趋于无限,没有终止时间,所以没有终值,只有现值。
(三)年金现值(P)
1.普通年金现值
(1)普通年金现值:指普通年金中各期等额收付金额在第 1 期期初的复利现值之和。
(2)普通年金的现值计算公式为:

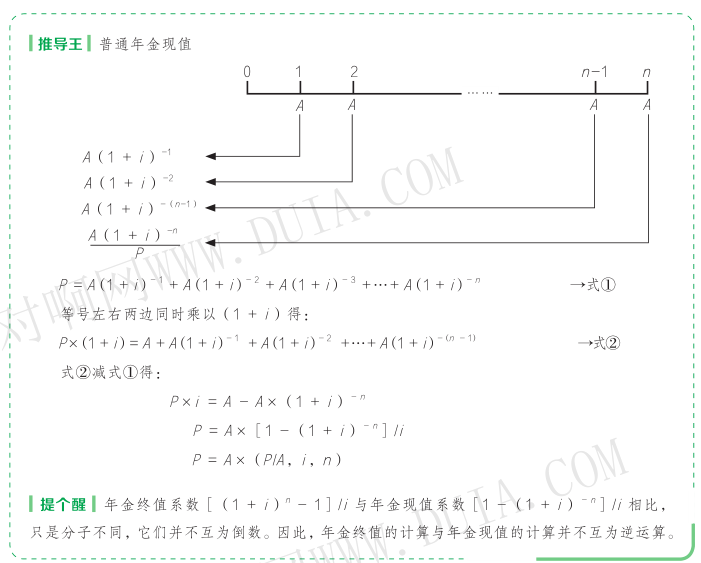

2. 预付年金现值
(1)预付年金现值: 指预付年金中各期等额收付金额在第 1 期期初的复利现值之和。
(2)预付年金现值的公式:
P = A ( P / A , i , n )×(1 + i )
或 P = A [( P / A , i , n - 1)+ 1](期数减 1,系数加 1)


3. 递延年金现值
(1)递延年金现值:是指递延年金中各期等额收付金额在第 1 期期初的复利现值之和。
(2)递延年金现值的三种计算方法,假定最初有 m 期没有收付款项,后面 n 期每年有等额的系列收付款项。
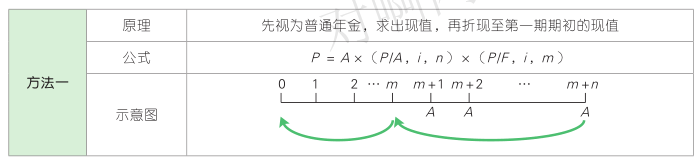


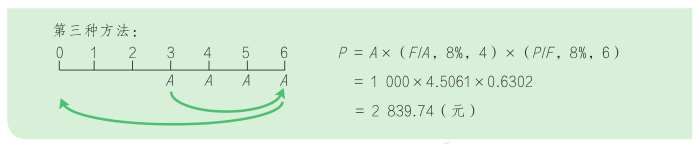
4. 永续年金现值
(1)永续年金现值可以看作一个 n 趋于无穷大时普通年金的现值。
(2)永续年金现值计算公式如下 :


(一)年偿债基金
年偿债基金,指为了在约定的未来某一时点清偿某笔债务或积聚一定数额的资金而必须分次等额形成的存款准备金。也就是为使年金终值达到既定金额的年金数额(即已知终值 F ,求年金 A )。
在普通年金终值公式中解出 A ,这个 A 就是年偿债基金。


(二)年资本回收额
年资本回收额是指在约定年限内等额回收初始投入资本的金额。年资本回收额的计算实际上是已知普通年金现值 P ,求年金 A 。
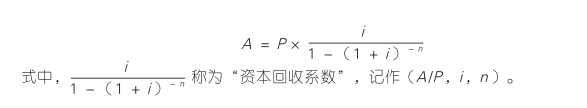

(一)现值或终值系数已知的利率计算
具体操作步骤如下:
(1)查阅相应的系数表,如果能在表中查到相应的数值,则对应的利率就是所求的利率。
(2)如果无法在系数表中直接查到对应数值,则采用插值法(或内插法)来辅助计算得出。
复利计息方式下,利率与现值(或者终值)系数之间存在一定的数量关系。已知现值(或者终值)系数后,可以通过插值法计算对应的利率。
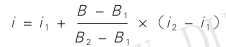
式中,所求利率为 i , i 对应的现值(或者终值)系数为 B , B 1 、 B 2 为现值(或者终值)系数表中与 B 相邻的系数, i 1 、 i 2 为 B 1 、 B 2 对应的利率。


(二)现值或终值系数未知的利率计算
如果一个表达式中含有两种系数,在这种情况下,现值或终值系数是未知的,无法通过查表直接确定相邻的利率,需要借助系数表,经过多次测试才能确定相邻的利率。


(三)实际利率计算
1.一年多次计息时的名义利率与实际利率
如果以“年”作为基本计息期,每年计算一次复利,这种情况下的实际利率等于名义利率。
如果按照短于一年的计息期计算复利,这种情况下的实际利率高于名义利率。
名义利率与实际利率的换算关系如下 :
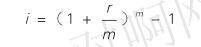
其中, i 为实际利率; r 为名义利率; m 为每年复利计息次数。

2. 通货膨胀情况下的名义利率与实际利率
(1)名义利率是央行或其他提供资金借贷的机构所公布的未调整通货膨胀因素的利率,即利息(报酬)的货币额与本金的货币额的比率,即指包括补偿通货膨胀(包括通货紧缩)风险的利率。实际利率是指剔除通货膨胀率后储户或投资者得到利息回报的真实利率。
(2)名义利率与实际利率之间的关系为 : 1 +名义利率=(1 +实际利率)×(1 +通货膨胀率),所以,实际利率的计算公式为 :


沙发已就位,请评论后上座
加载失败,请刷新当前页面再试试!
{{replyList.forUserName}}:
Duia_{{replyList.forUserId}}:

快来登录发表你的精彩评论啦

发帖
回复
选择需要转移到的吧组
选择需要转移到的吧组分类